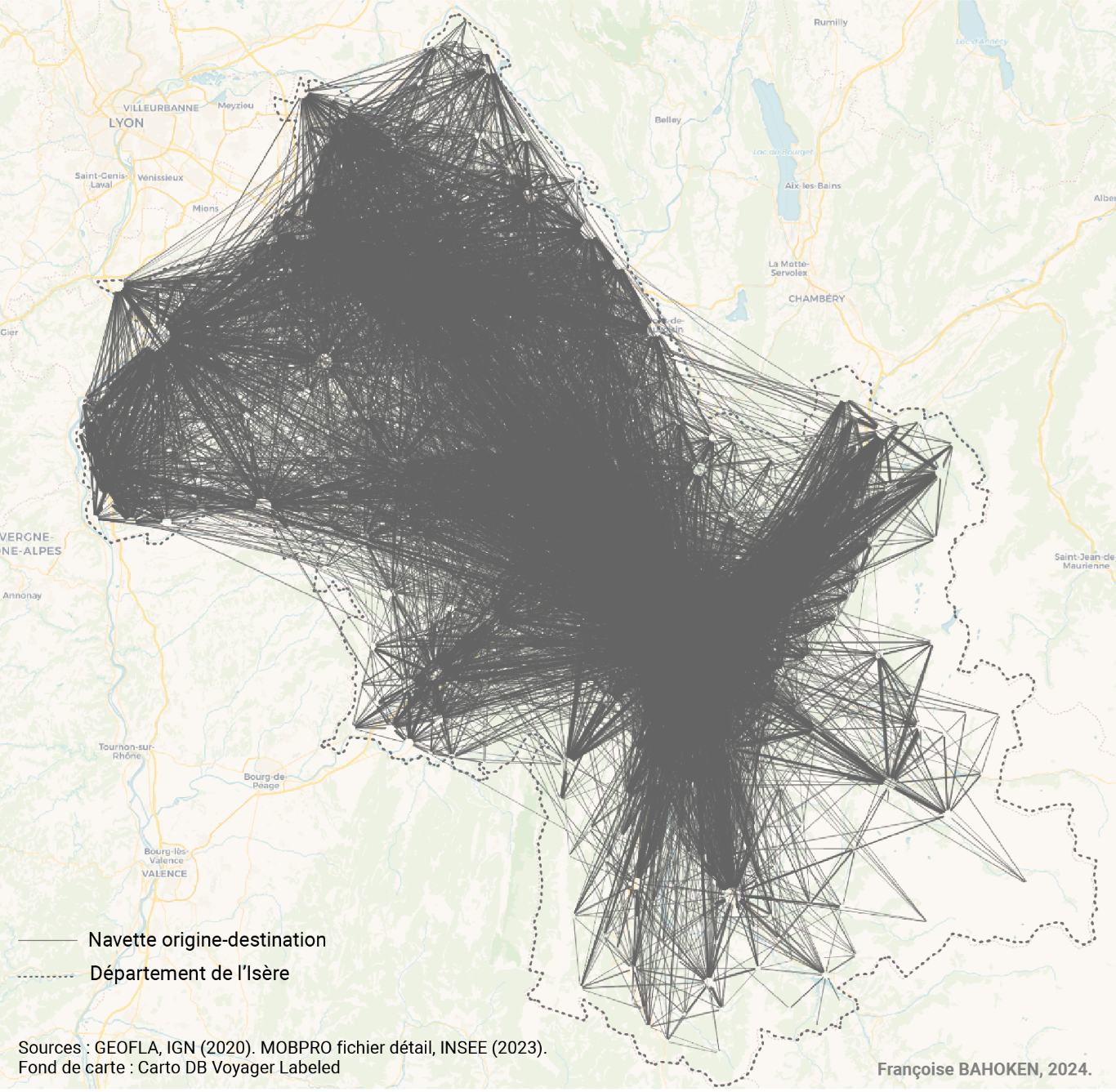
Mapping local mobility through “proximity flows”

Françoise Bahoken
〉Chargée de recherches
〉Univ. Gustave Eiffel, IFSTTAR
〉AME-splott

〉francoise.bahoken@univ-eiffel.fr

〉article long 〉

Télécharger l'article. 4-2024 Bahoken

Résumé : En raison de la surcharge graphique (ou effet spaghetti) observée sur les cartographies des mobilités spatiales impliquant plus d’une dizaine de lieux, l’information portant sur les déplacements nécessite d’être filtrée ou réduite en amont de l’étape de représentation et cela, quelle que soit l’échelle des mobilités à représenter. Si plusieurs approches du filtrage sont envisageables, celle proposée ici est exogène à la matrice et prend en compte l’espace géographique des mobilités. La procédure de filtrage agit en effet d’abord sur l’espace des lieux d’origine ou de Destination (OD) des flux, avant d’être appliqué aux interactions proprement dites. L’espace est alors appréhendé dans le cadre de différentes approches théoriques mises en œuvre pour cartographier autant de type de flux de mobilités de proximités. La première est continue et représente les mobilités de courte distance euclidienne ; la seconde est discrète, elle mobilise le voisinage des OD fondé sur la notion de contiguïté pour cartographier des flux de proximité territoriale ; la troisième est mixte et combine des approches discrètes et continues pour cartographier des mobilités locales, selon une proximité de voisinage spatial.

Mots-clés : cartographie, mobilités spatiales, carte de flux, distance, voisinage, flux de proximité

Abstract: Because of the graphic complexity (or spaghetti effect) observed on flow maps involving more than a dozen locations, information about movements needs to be filtered or reduced before the representation step, whatever their scale. While several filtering approaches are possible, the one proposed here is exogenous to the matrix and takes into account the geographical space of mobilities. Indeed, filtering first acts on the space of flows’ places of origin or destination (OD) before being applied to the interactions themselves. The geographic space is then apprehended within the framework of different theoretical approaches implemented to varied local flow maps. The first approach is continuous and represents mobility over short Euclidean distances; the second is discrete, mobilizing OD neighborhoods based on the notion of contiguity applied to flow mapping territorial proximity flows; the third is mixed, combining discrete and continuous approaches to flow mapping local mobilities, according to spatial neighborhood proximity.

Key-words: maps, flowmaps, spatial mobilities, distance, neighborhood, proximity flows

1 Introduction

Les mobilités spatiales présentent la particularité de pouvoir être appréhendées du point de vue des localisations et/ou de celui des interactions exprimées entre les lieux mis en relation. Lorsqu’elle est menée au niveau global, l’analyse s’intéresse dans le premier cas à la géographie des lieux impliqués dans la mobilité dont il est question, qu’il s’agisse de ceux de départ (d’origine) et/ou de ceux d’arrivée (de destination). Il s’agit alors de les différencier en fonction de leurs caractéristiques structurelles (la population résidente ou l’offre d’emploi par exemple) ou bien fonctionnelles à savoir celles qui résultent de leur mise en relation. Dans le second cas, l’analyse s’intéresse aux liens, c’est-à-dire à la mise en relation de lieux d’origine-destination (OD) pour appréhender les déplacements proprement dit – en complément de leurs effets sur la différenciation des lieux –, en révélant par exemple des processus de coopération entre les couples de lieux OD.

A ces deux grandes focales de l’analyse globale des mobilités spatiales (du point de vue des lieux et/ou des liens) correspond deux parties de la matrice OD qui archive les données statistiques correspondantes, respectivement les marges et le cœur de la matrice.

Figure 1. Focales d’analyse d’une matrice OD au niveau global

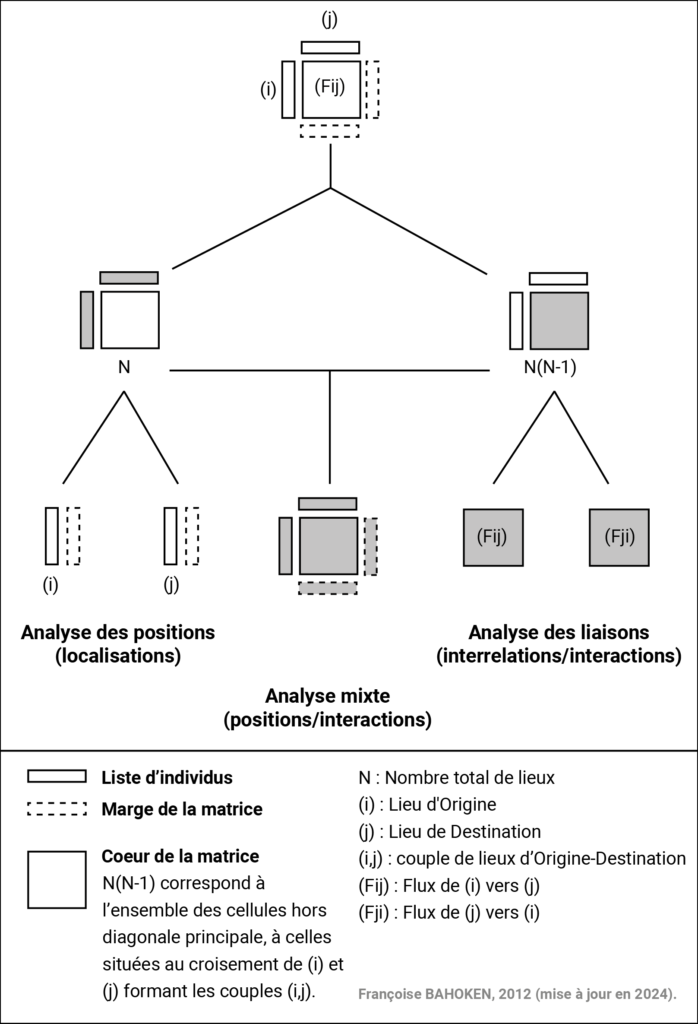
Ainsi, dès lors que le nombre N de lieux impliqué augmente, la taille du système de mobilité correspondant accroit de manière quadratique, puisque N(N-1) liens – sans compter l’information éventuellement disponible sur la diagonale principale de la matrice OD qui correspond ici aux déplacements intra zonaux – doivent être mobilisés pour analyser les seuls déplacements.

Cette situation ne poserait pas de problèmes si elle ne générait pas un effet spaghetti caractéristique d’une surcharge graphique des cartographies des interrelations ou des interactions correspondantes. Pour dix lieux analysés, 10 (10-1) liens soit 90 lignes seraient à représenter en complément de l’information portant sur les dix lieux. En effet, aux deux grandes focales d’analyse de la matrice OD correspondent deux grandes méthodes de représentation graphique et cartographique de l’information disponible (du point de vue des lieux ou des liens), chacune d’entre elles pouvant par ailleurs faire l’objet de plusieurs classes de représentation en fonction de considérations théoriques, méthodologiques ou thématiques suivant l’intention du cartographe. Aussi en fonction de la manière dont l’espace géographique est appréhendé.

La cartographie des N(N-1) liens du système de mobilité spatiale prend ainsi la forme de carte de flux ou de mouvements qui revêtent ceci de particulier qu’elles nécessitent de sélectionner ou de réduire l’univers de l’information à représenter et cela, au préalable de la représentation proprement dite. Pour y parvenir, plusieurs approches sont envisageables parmi lesquelles celles qui consistent à agir sur les données numériques, en filtrant les interactions spatiales de manière à ne représenter que celles qui sont jugées significatives au regard de l’objectif de la carte. La significativité en la matière nécessite aussi plusieurs arbitrages (Bahoken, 2014, 2017). Au niveau global du système d’échanges, la sélection conduit à l’application d’un critère unique (α) qui articule deux des principaux objectifs de la représentation des flux/mouvement : la cartographie d’une part significative du total des interactions et la densité faible de liens sélectionnés pour assurer la clarté de la figure.

Les méthodes usuelles de filtrage des flux fondées sur les valeurs numériques conduisent à des cartes qui ne considèrent pas nécessairement l’espace géographique des mobilités spatiales dans la construction, ce dernier étant tout au plus mobilisé comme fond de carte, c’est-à-dire des fins d’habillage de l’image et non comme variable. Dans une logique de flux, l’espace support des mobilités spatiales à cartographier n’est en effet pas considéré comme une variable d’ajustement de la modélisation graphique, quand bien même ce même espace serait pris en compte dans la modélisation numérique. Et pourtant, si l’on s’en tient au registre du filtrage des déplacements à représenter, la prise en compte de cet espace dans le processus de construction cartographique va considérablement enrichir considérablement l’image de ces mobilités. La raison tient au fait que la cartographie d’une matrice formée de couples d’OD localisées est susceptible de varier à la fois en fonction de l’acception de la séparation entre ces lieux (Bahoken, 2016) et de l’échelle géographique d’observation de ces mobilités. Dit autrement, la prise en compte des positions relatives des OD les unes par rapport aux autres à une échelle géographique donnée, en l’occurrence de leurs espacements (pour ne pas dire de leurs éloignements) va permettre de cartographier des flux qui s’expriment à proximité, à courte distance ou entre des lieux proches en les distinguant de ceux qui sont observés à longue distance.

Je vais appréhender cette contrainte de localisation des OD imposée par l’espace géographique, par le prisme de la notion de distance parcourue entre les lieux. L’analyse cartographique proposée dans cet article va ainsi considérer l’espacement relatif des OD pour filtrer les données de flux (Fij) à cartographier afin de réduire l’effet spaghetti. Sachant que la cartographie des interactions spatiales observées dans l’espace géographique mobilise trois formes distinctes de distances^[1] (Bahoken, 2016), je fais l’hypothèse d’être dans la situation idéale de corrélation quasi parfaite entre les distances empiriques, euclidiennes et cartographiques (Bahoken, 2016 : 272).

L’objectif de ce papier est de montrer le rôle joué par l’espace géographique dans l’analyse cartographique des mobilités spatiales par des flux OD qui s’expriment à courte distance ou à proximité. L’analyse va être illustrée par les mobilités professionnelles de l’Isère que je présente dans un premier temps. Leur matrice OD étant soumise à un effet spaghettifort, son filtrage va être réalisé par l’espace des OD, que j’appréhende ici selon les trois paradigmes suivants : dans le cadre d’une approche continue, mobilisant la métrique euclidienne kilométrique pour représenter des mobilités de courte distance ; ensuite dans le cadre d’une approche discrète requérant une métrique de voisinage fondée sur la notion de contiguïté territoriale pour cartographier des flux de proximité ; enfin, dans le cadre d’une approche mixte (discrète/continue) fondée sur une proximité de voisinage spatial.

2 Présentation des données et des prérequis théoriques et méthodologiques

J’ai recours à titre d’illustration au fichier Mobilités professionnelles (MOBPRO) issues des données collectées en 2020 et publiées en 2023 par l’INSEE. Les données décrivant les navettes intercommunales de l’Isère sont présentées dans un premier temps. Le second temps décrit la posture théorique et méthodologique adoptée pour cartographier les mobilités spatiales de l’Isère locales, de courte distance ou de proximité à partir de tableaux exogènes : des matrices de distance et de voisinage.

2.1 Les mobilités professionnelles de l’Isère

Si le département de l’Isère est composé de 533 communes, seules 511 d’entre elles sont impliquées dans le système intra départemental de navettes inter communales domicile-travail. Pour les besoins de l’analyse, j’ai en effet préalablement fermée cette matrice asymétrique, pour la limiter aux flux échangés entre les 511 communes du département. Elle présente également une forte densité, avec 95% de cases renseignées, ce qui correspond à 13 349 liens effectifs à cartographier. Sa représentation cartographique directe souffre d’un effet spaghetti important qui rend la figure illisible (voir Figure 2).

Figure 2. Ensemble des navettes de l’Isère (2023)

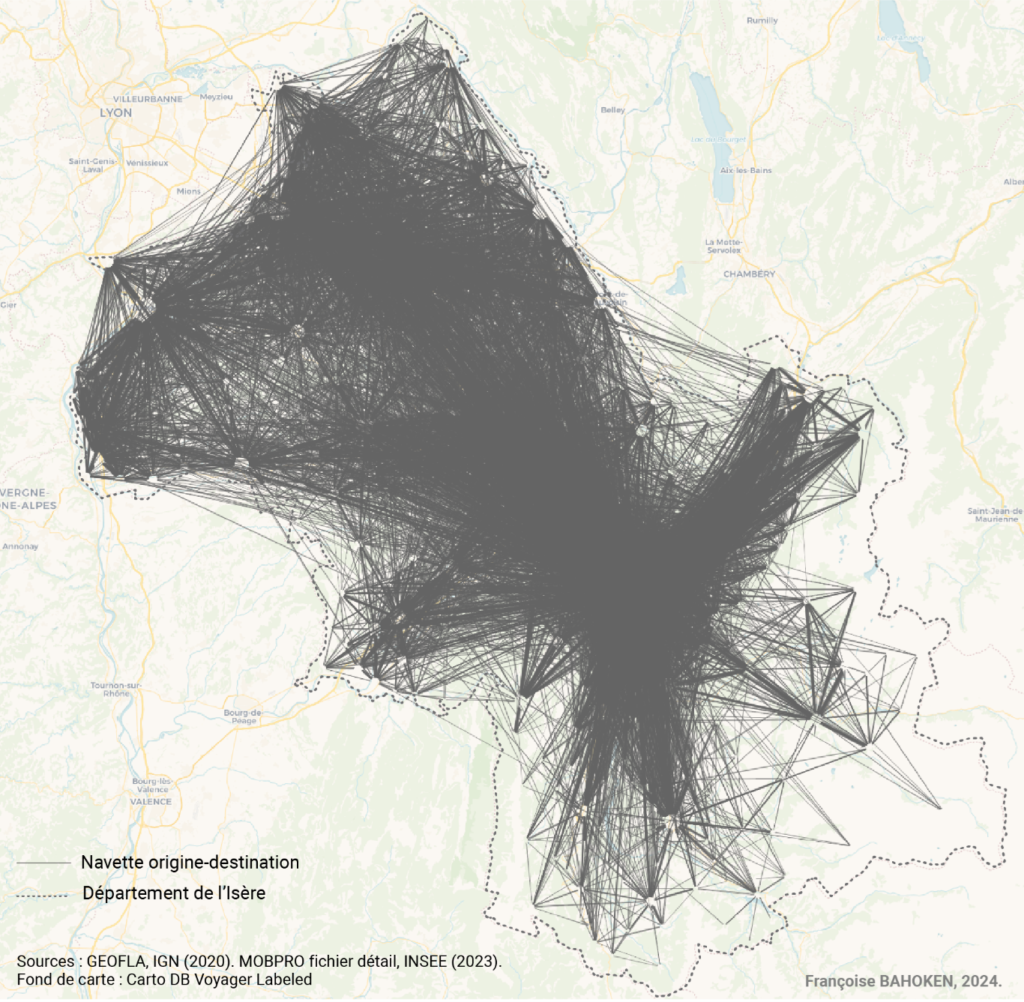
Pour affiner cette cartographie, il convient de filtrer cette matrice et pour cela, décider d’un seuil d’interactions (ou d’un intervalle) à partir duquel les liens correspondants à ces flux seront préservés sur la carte – et en deçà ils seront éliminés, pour être considérés comme non significatifs.

Plutôt que filtrer ces flux en fonction d’un critère fondé sur leur valeur numérique, je vais les sélectionner en fonction d’un critère géographique permettant de séparer les mobilités locales ou de proximité, des mobilités à plus longue distance. L’approche va ainsi considérer l’espace géographique de ces flux par le prisme de la distance parcourue, qui va être appréhendée suivant différents cadres théoriques.

2.2 Prérequis théoriques et méthodologiques sur le filtrage numérique des flux

La méthode généralement utilisée pour filtrer les valeurs de flux consiste à leur appliquer un critère arbitraire visant à ne retenir que les n plus gros flux en valeur, par exemple, les n=10 plus gros flux, dont on sait qu’ils s’expriment à courte distance, en vertu de la première Loi de la géographie (Tobler, 1970). Le problème de cette méthode, pour efficace qu’elle puisse être, est qu’elle ne considère pas la géographie de ces flux, ce qui peut être préjudiciable à l’analyse de la proximité. C’est pourquoi il convient d’adopter une double posture : numérique, fondée sur les valeurs et géographique, relative à l’espace parcouru.

L’espace est appréhendé à l’aide d’une matrice d’information géographique, formée des (i) lieux de la zone d’études impliqués dans la matrice de flux (Fij), à partir de laquelle une matrice de distance, plus précisément, une matrice de séparation des lieux sera bâtie de manière à considérer la proximité des lieux impliqués dans le système de flux.

Sur le plan théorique, l’espace géographique des flux mobilisé dans l’analyse cartographique des flux que je propose est appréhendé par le prisme de la distance parcourue. Celle-ci est définie en termes d’éloignement ou en termes de proximité des lieux, en fonction de la métrique sous-jacente. Trois matrices de séparation des lieux vont par conséquent être mobilisées, en fonction de la manière dont cet espace des flux est considéré. La première d’entre elles est une métrique continue recourant à la distance euclidienne (pour simplifier) parcourue par ces flux (Dij) ; elle est exprimée en kilomètres. La seconde matrice est une métrique discrète, fondée sur la notion de contiguïté (Ckij) des mailles de la zone d’étude, pour définir un voisinage de lieux formé de leur k-contiguïté. À la différence de la précédente matrice qui est continue, la matrice de voisinage est ordinale, car elle exprime un nombre k de limites de zones à franchir pour rejoindre un lieu de destination (j) depuis un lieu d’origine (i). La troisième matrice est mixte, combinant les approches discrètes considérant à la fois un maillage territorial en k-contiguïtés et une distance kilométrique à parcourir (Ckij^k). Ces trois matrices permettent la représentation respective de flux s’exprimant à courte distance, dans leur voisinage territorialde contiguïtés d’ordre 1 ou k, ou encore dans un voisinage spatial.

Sur le plan méthodologique, le critère de filtrage spatial ou territorial, de la courte distance ou de la proximité, issu de l’une de ces trois approches va être appliqué en première instance sur la matrice de séparation des OD et en seconde instance sur celle des flux. Cela implique que le filtrage des flux va en pratique reposer sur la réduction d’une matrice exogène (l’une ou l’autre matrice de séparation) ce qui, dit autrement, signifie que l’espace géographique d’expression des flux va servir à les filtrer de manière à assurer la clarté de l’image des flux correspondante. À noter que cette approche peut être vue comme une adaptation au cas des flux OD, des discrétisations reposant sur la courbe clinographique^[2].

L’espace géographique est mobilisé dans deux familles de matrices de séparation des lieux qui correspondent à deux paradigmes théoriques : une matrice de distance et deux matrices de voisinage. Toutes deux autorisent le calcul d’un ensemble de mesures d’espacement sur la géométrie/géographie de la même zone d’étude, dont je vais montrer qu’elle varie en fonction du paradigme sous-jacent.

La matrice de distance s’appuie sur une vision continue de l’espace, elle associe des données quantitatives continues à une implantation spatiale géométrique bi-ponctuelle (les coordonnées XY des lieux OD ainsi reliés par l’existence d’un flux) et à une implantation spatiale graphique linéaire (la ligne tracée entre les OD et perçue comme telle sur la carte, qui symbolise graphiquement la navette). Les matrices de voisinage sont, quant à elles, fondées soit sur une approche discrète de l’espace, partitionné en zones ; elles associent des données qualitatives ordinales à des implantations spatiales géométriques et graphiques aréolaires (ou surfaciques), soit sur une approche mixte aréolaire et linéaires.

La représentation des mobilités professionnelles de l’Isère, selon ces deux paradigmes discrets/continus, va générer plusieurs collections de k cartes qui résultent d’une réduction des flux opérée soit en fonction de leur distance kilométrique parcourue (en k classes de distances), de leur voisinage territorial ou bien spatial (en contiguïtés d’ordre k et/ou kilométrique). Plutôt que de présenter cette collection de k cartes, il me semble plus intéressant d’examiner la manière dont la représentation de ces navettes va changer en fonction de la manière dont l’objectif de la carte, de représenter des flux locaux parce qu’ils sont proches ou non est mise en œuvre.

3 La métrique continue, fondée sur la représentation de flux à courte distance

Pour représenter la courte distance, j’ai recours à une matrice de distance kilométrique euclidienne classique, calculée entre les communes de l’Isère, sur laquelle j’applique un unique critère de filtrage global ; ce dernier va creuser cette matrice dans des proportions qui vont être répercutées sur la matrice de flux.

La procédure s’apparente à une discrétisation exogène^[3], car les bornes des classes de flux sont déterminées en fonction de la série des distances. Cette méthode présente l’intérêt, non négligeable dans notre cas, de ne pas nécessiter de transformation de la série, par exemple pour la normaliser ; sachant que les distributions des flux et de leurs distances ne suivent pas la Loi normale. Deux approches sont traditionnellement envisagées pour déterminer les bornes de distance. La première consiste à appliquer un critère intuitif, issu de dires d’experts sur la thématique dont il est question, afin que la mesure d’éloignement retenue soit la plus pertinente possible. Pour saisir les mobilités locales, il est ainsi possible de considérer un seuil fondé sur la distance parcourue, tel celui de 100 kilomètres régulièrement cité par J-P. Orfeuil pour qualifier ces mobilités locales (voir par exemple Orfeuil, 2015) ; ou encore le « potentiel de contact » entre deux lieux calculé par A. L’hostis & al. (2004) et fondé sur une double mesure de distance-temps de transport. Ces mesures sont calculées soit sur le réseau de transport ou approximées par la distance euclidienne (Dij).

La seconde approche consiste à déterminer ce seuil en fonction de critères endogènes à la série statistique. En effet, la matrice (Dij) étant définie sur un intervalle réel [(Min(Dij) ; Max(Dij)], en unités kilométriques, son format continu autorise sa discrétisation en k classes de distances ; chacune des bornes correspondant à un paramètre pour segmenter la matrice (Fij), également en k classes de valeurs de flux selon la distance kilométrique parcourue. Le choix de cette approche conduit ensuite à décider de la manière dont les valeurs des bornes (Min) et (Max) des k classes vont être estimées, dans notre cas seule la borne (Max) et cela, en fonction de la forme de la série et de l’objectif de la carte. Tobler (1987) suggère d’utiliser la moyenne ( ) des flux en première intention. Je reprends cette idée d’utiliser les valeurs centrales de la série, mais en les appliquant à la matrice des distances.

La matrice en question étant dissymétrique, la forme de son histogramme tout comme celle des distances, ce qui est logique : elles recèlent beaucoup plus de liaisons présentant des valeurs fortes que des valeurs faibles. Cette non normalité statistique a pour conséquence que les méthodes de discrétisation qui postulent la normalité de la série, ne sont pas directement applicables ; elles nécessitent une transformation des données. Pour éviter cette opération supplémentaire, je fais le choix d’utiliser des méthodes de discrétisation ne postulant pas cette normalité, tout en mobilisant les paramètres de tendance centrale. Il s’agit en l’occurrence des moyennes emboitées et des quantiles, mobilisant respectivement la moyenne arithmétique ( ) et la médiane (Q2), deux méthodes de type statistique qui « reposent sur une étude des fréquences et non des valeurs de la variable » (Cauvin et al., 1987 : 37). Toutes deux conviennent de fait à notre objectif de ne représenter que les petits flux entre des lieux peu espacés, ou les plus faibles de matrices ordonnées.

3.1 La moyenne géométrique des distances parcourues, comme critère de sélection des flux de courte distance

La moyenne arithmétique ( ) étant un paramètre de tendance centrale bien connu, il est facile de l’utiliser pour filtrer les flux qui le seront alors selon la distance moyenne parcourue, en recourant aux moyennes emboitées.

Cette méthode de partition selon une progression arithmétique a été mise au point par Scripter en 1970 pour les séries asymétriques. Elle génère des valeurs moyennes emboitées successives pouvant servir de bornes pour discrétiser une série en un nombre pair de classes, idéalement 4 ou 8 classes. Sur le fond, la méthode s’apparente aux quantiles (voir infra), en particulier lorsque la distribution ne présente pas de valeurs extrêmes exceptionnelles. Elle évoque aussi la discrétisation selon la progression géométrique, qui permet d’avoir plus de classes dans les petites valeurs, une caractéristique utile pour les distributions asymétriques telle celles des flux et de leurs distances. Il y a en effet beaucoup plus de navettes présentant des valeurs faibles mais qui s’expriment à longue voire à très longue distance ; cela caractérise d’ailleurs l’effet de couverture spatiale, l’un des critères de définition de l’effet spaghetti (voir Bahoken, 2015).

Le recours à la moyenne rend cependant la méthode sensible aux valeurs extrêmes, mais la matrice de distances euclidiennes ne comporte pas de trous dans sa distribution et pour cause : il est toujours possible de mesurer la distance kilométrique entre deux lieux (voir Figure 3).

Figure 3. Résumé des distances discrétisées suivant des moyennes emboitées

Une discrétisation en (k=4) classes de distances (Dij) des communes de l’Isère, selon les moyennes emboitées : la distance moyenne parcourue étant de 12,9 kilomètres, on obtient les quatre bornes suivantes : 0,13 km ; 6,54 ; 12,9 km et 63,5 km ; la distance maximale de 114,6 kilomètres. Partant de là, il est possible de réaliser de réaliser plusieurs séries de cartes permettant de sélectionner celles qui correspondent aux navettes de courte distance :

une première série de deux cartes comporterait deux cartes : l’une décrivant les flux ayant parcouru moins de 13 kilomètres et l’autre ceux ayant parcouru plus de 13 kilomètres;
une seconde collection serait composée de cartes représentant successivement les flux ayant parcouru moins de 6 kilomètres, ceux ayant parcouru moins de 13 kilomètres et moins de 63 km kilomètres ;
Une troisième série serait également composée de cartes décrivant les flux compris entre 0,1 kilomètres et 6 kilomètres, ceux compris entre 6 et 13 km kilomètres et ceux entre 13 et 63 kilomètres ;
etc.

Pour illustrer mon propos et puisqu’il faut choisir, la Figure 3 présente une série trois cartes qui, toutes, apportent une vision cartographique des navettes de courte distance de l’Isère – ces dernières étant sélectionnées selon une approche continue fondée sur les moyennes emboîtées. Pour faciliter la lecture, les liens symbolisant les navettes ne sont pas pondérés sur la Figure 4.

Figure 4. Les navettes parcourant les plus courtes distances (moins de 13 kilomètres)

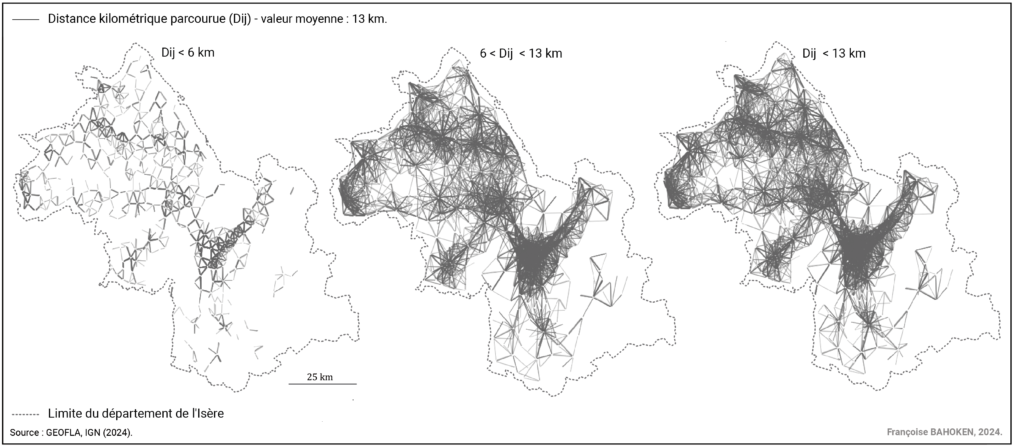
La méthode des moyennes géométriques revêt « (…) deux propriétés souhaitables, [des] fréquences également réparties dans les classes et étendues de chaque classe assez proches (Evans, 1977), mais en établissant des intervalles assez étroits pour les zones modales et assez larges pour les secteurs de faibles fréquences. Elle évite les classe vides même s’il existe des discontinuités dans la série et ne donne pas une importance prédominante aux valeurs extrêmes » (Cauvin et al. 1987 : 42).

Une autre méthode consiste à s’appuyer sur un critère de position, en l’occurrence sur les quantiles pour représenter la même courte distance.

3.2 Le premier quartile comme critère de position des flux de courte distance

Le choix des quantiles, fondés sur la médiane à savoir le second quantile (Q2), comme valeur centrale apparaît souvent à tort comme un choix par défaut, alors qu’il est particulièrement pertinent pour représenter ces mobilités locales, de courte distance, dans le cadre d’une approche continue. Il est ainsi possible de calculer différents quantiles qui serviront de bornes de discrétisation (voir Figure 5).

Figure 5. Résumé des distances discrétisées suivant des quantiles

L’intérêt des quantiles est qu’ils permettent de raisonner en termes de pourcentage de mobilités présentant les distances les plus faibles, ce qui facilite à mon sens grandement l’interprétation qualitative des cartes. Ils entraînent ainsi la représentation des mobilités parcourant une distance inférieure à la médiane, à savoir 9,6 kilomètres (10 en valeur arrondie), ainsi que ceux parcourant 25% des distances les plus faibles, soit moins de 4 kilomètres qui correspondent au premier quartile ou encore ceux parcourant moins de 18 kilomètres correspondant aux 75% de distances les plus faibles (voir Figure 6).

Figure 6. Les parts en pourcentage de navettes parcourant les plus courtes distances

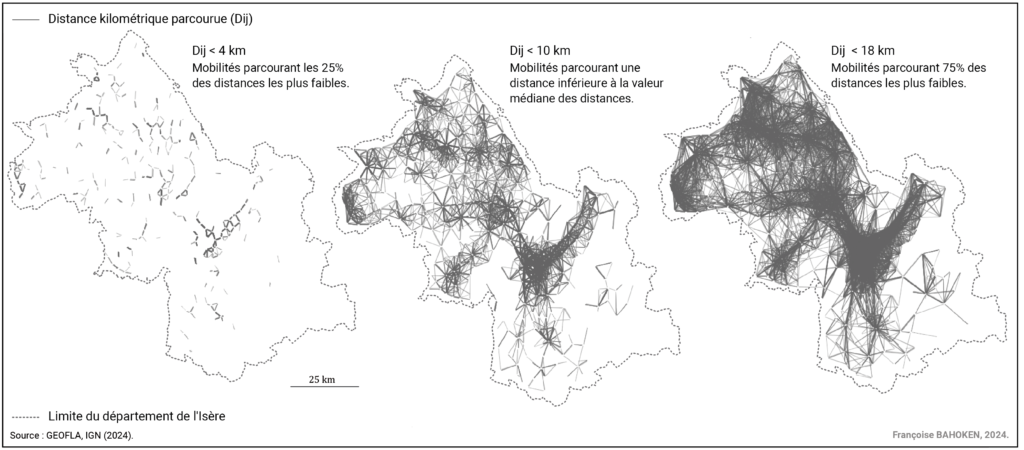
Le fait que la méthode des quantiles génère des classes d’effectifs égaux peut poser différents problèmes qui résultent d’un filtrage des flux (Fij) construit sur la série des distances kilométriques parcourues à vol d’oiseau (Dij). En effet, l’une des conséquences de cette approche réside dans la forte variation de la fréquence des valeurs de chacune des classes de flux, en raison de la relation inverse entre la valeur de flux et la distance parcourue – puisque plus le flux est fort et moins la distance parcourue est grande. C’est la raison pour laquelle, les cartes de flux les plus lisibles sont celles pour lesquelles la distance parcourue est inférieure à la distance médiane (Dij < 10 km), comme présenté sur la Figure 5.

Ces critères de sélection des flux à représenter, parce qu’ils sont fondés sur les valeurs centrales (moyenne et médiane) de la série sont considérés comme robustes. Ils s’appuient sur une vision continue de l’espace, décrivant l’éloignement exprimé en kilomètres. Ils ne permettent pas de représenter des flux locaux de proximité en tant que tels, définis comme ceux ayant lieu dans un voisinage donné. Pour ceux-là, il convient de raisonner selon une approche discrète de l’espace.

4 La métrique discrète, fondée sur la proximité de contiguïté des flux locaux

Le caractère discret de l’espace est établi en lien avec un maillage territorial, en l’occurrence celui des communes de l’Isère. Ce maillage est fondamental dans le cas des flux, car il sert de support à leur définition, par le recours à la notion de franchissement de limite de zone (les flux que j’étudie sont intercommunaux, car tous ont franchi une des limites communales du département de l’Isère). Aussi est-il intéressant de prendre en compte ce maillage pour définir les flux locaux qui se produisent dans un voisinage territorial donné.

Ce raisonnement sur le maillage territorial de l’espace des flux fait référence au voisinage topologique des lieux. C’est la raison pour laquelle la proximité est appréhendée ici comme une mesure de séparation discrète, car elle s’appuie sur une partition de l’espace en zones présentant des implantations spatiales géométrique et graphique nécessairement aréolaires. Ce qui m’importe ici, ce n’est pas tant la morphologie des zones (hétérogénéité/homogénéité des mailles) que la position de leurs limites – conférant ainsi à l’espace son caractère discret.

Cette mesure de proximité discrète est un critère de sélection des flux qui s’appuie sur la notion de contiguïté (ou d’adjacence) territoriale en fonction des limites de zones. Elle est fondamentale en analyse spatiale, car elle est susceptible d’engendrer un effet d’interaction spatiale entre les OD. C’est d’ailleurs l’une des hypothèses des modèles gravitaires selon laquelle l’intensité des flux est d’autant plus importante que les lieux sont proches et, dans le cas présent, qu’ils sont contigus, partagent ou sont séparés par une ou plusieurs frontières communes. « La contiguïté est la propriété d’objets ou de lieux qui sont voisins, qui se touchent, parce qu’ils ont une frontière commune s’il s’agit de mailles ou de zones, ou qui sont connectés par une ligne, une voie de communication s’il s’agit de nœuds dans un réseau » (Pumain, Saint-Julien, 2005 : 29).

Le recours à la contiguïté va me permettre de montrer comment la prise en compte de ce critère d’éloignement permet de révéler cet effet de voisinage caractérisant les flux à proximité ; il est défini selon deux modalités : l’une par le caractère limitrophe des flux observés dans leur voisinage territorial immédiat, c’est la contiguïté simple ; l’autre modalité de voisinage est fondé sur une contiguïté ordinale où flux relie deux lieux proches mais non limitrophes.

4.1 La contiguïté binaire des flux observés entre zones limitrophes (Cij=1)

La contiguïté simple (Cij) est la mesure du caractère limitrophe de deux lieux (i) et (j) qui sont adjacents ou partagent une frontière commune. Cette mesure étant binaire, (Cij=1) si (i) et (j) sont limitrophes et séparées par une frontière de longueur non nulle (Cij 0) – ce qui justifie le recours à une implantation spatiale géométrique surfacique, sinon à 0.

W. Tobler (1987) suggéra l’utilisation d’un tel critère pour clarifier l’image de flux représentant des mobilités locales. En considérant une matrice de migrations, l’auteur mentionne que leurs flux seront alors « […] réorientés [donc filtrés] pour ne passer que dans des zones adjacentes. Ceci peut être réalisé de différentes manières, mais le résultat final est le même ; la carte de mouvement ne contient pas de bandes ou de flèches qui se chevauchent » (Tobler, 1987 : 162).

L’intérêt de la sélection des flux selon leur caractère limitrophe ou non est que la carte apporte une information que l’on ne possède théoriquement que partiellement. En effet, les mobilités intra zonales sont en pratique perdues lorsque la diagonale de la matrice est portée à zéro, puisque la carte représente des flux inter zones. La cartographie des seuls flux qui se produisent entre des zones contigües conduit alors à un changement d’échelle qui permet de retrouver, certes partiellement, une information sur ces flux intra zonaux qui sont ceux étant très proches, tout en conservant l’information sur les flux inter zonaux qui correspond au niveau d’analyse.

Les flux locaux ne s’exprimant pas nécessairement entre zones adjacentes, il est possible d’augmenter la portée de ces flux voisins limitée à 1, en recourant à la contiguïté ordinale, sans pour autant représenter la longue distance.

4.2 La contiguïté ordinale des flux distants de (k) limites de zones (Ckij)

La contiguïté ordinale (Ckij) est une généralisation de la mesure de contiguïté simple à l’existence d’au moins deux limites de zones de longueurs non nulles à franchir pour atteindre un lieu de destination. Introduite par L. Lebart en 1969 pour analyser l’auto corrélation spatiale, cette mesure permet de considérer des proximités d’ordre (k=2, 3, …, n) qui sont issues du calcul de plus courts chemins sur un graphe, qui décrit le voisinage des lieux (généralement de leur barycentre) impliqués dans le système d’échanges.

La construction de cette matrice de contiguïté ordinale résulte du dénombrement du nombre de limites de zones à traverser entre deux 0D. Elle peut être représentée graphiquement par un graphe de voisinage de contiguïté ordinaleprenant des valeurs entières comprises entre 1 et +∞, si le graphe est non connexe. 28 graphes de voisinages des communes de l’Isère peuvent ainsi être construits, ceux d’ordres k=1 et k=2 évoquent le voisinage, avec respectivement 1 et 2 limites de zones à franchir pour atteindre une commune de destination depuis une commune d’origine (voir Figure 7).

Figure 7. Graphes de voisinage d’ordres 1 et 2 des communes de l’Isère

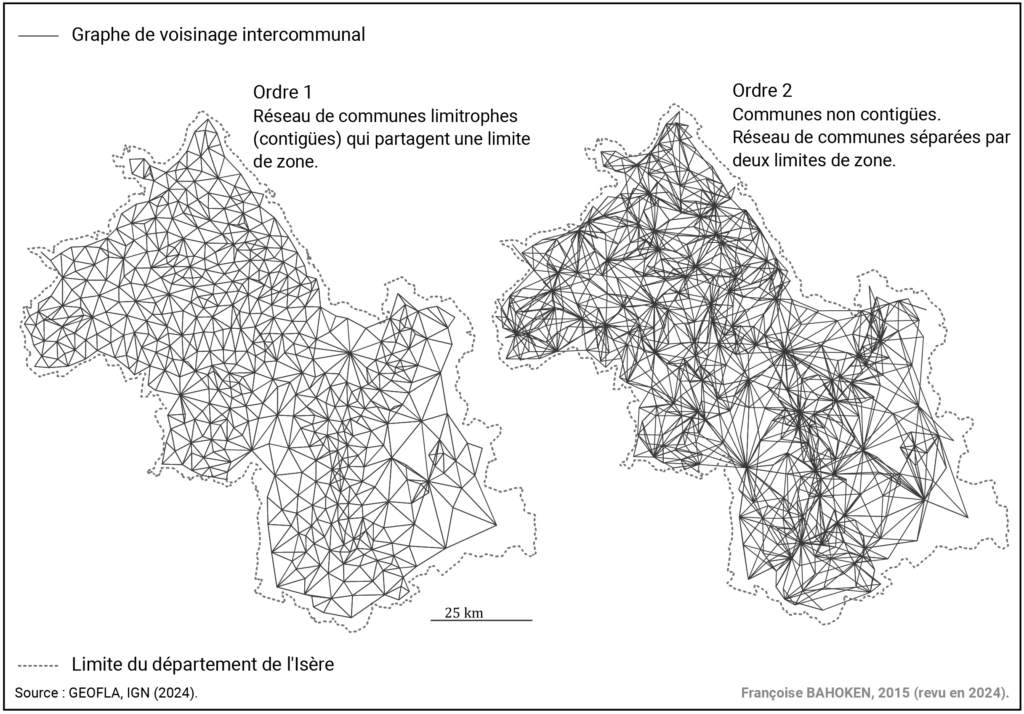
W. Tobler (1987) suggère que les mobilités locales – l’auteur ne mentionne pas le terme de proximité – s’expriment en réalité jusqu’à un nombre de k=4 limites de zones à franchir par un flux. Considérer différentes valeurs successives de k est une aide à l’interprétation non négligeable qui permet de visualiser les mobilités de proche en proches. « […] les interactions spatiales peuvent se propager dans l’espace de proche en proche, et pour l’analyse des ressemblances ou de la diffusion spatiale, on utilise souvent des matrices de contiguïté d’ordre deux, ou d’ordre trois, ou d’ordre n quelconque, qui représentent les possibilités de contact ou d’interaction entre des nœuds dans un réseau ou entre les mailles d’une grille, lorsqu’on accepte de franchir des écarts plus grands […]. On peut utiliser des matrices de contigüité pour calculer des distances topologiques, dites « mesures d’écarts, entre deux mailles quelconques d’une grille ou entre deux nœuds d’un réseau. On mesure alors le nombre de frontières à traverser, ou de segments à parcourir, pour se rendre d’un lieu à un autre. » (Pumain, Saint-Julien, 2005 : 31).

La matrice (Ckij) peut être appréhendée comme une proximité de contact si k=1 (CKij=1) définissant le voisinage immédiat de la contiguïté simple (Cij=1). Comme précédemment, il est possible de réaliser une collection de cartes de flux, ici de proche en proche. Les plus intéressantes pour notre examen des flux de proximité sont les cartes de flux entre zones limitrophes (contiguïté d’ordre 1) ou quasi limitrophes (ordre 2), présentées sur la Figure 8.

Figure 8. Navettes de proximité, effectuées entre communes (quasi) limitrophes

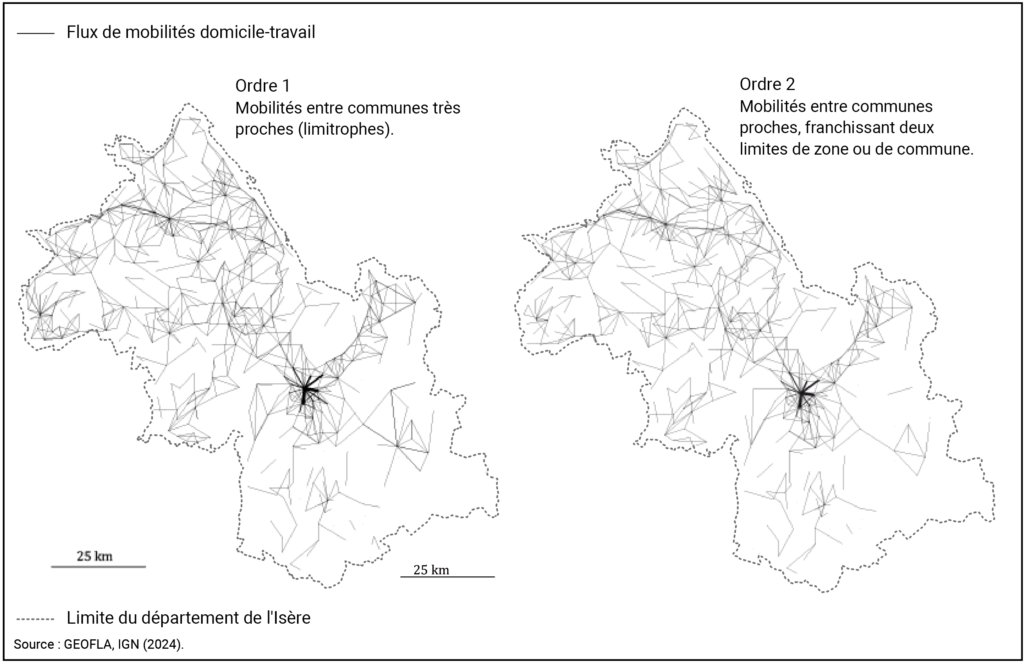
La Figure 7 décrit l’expansion des flux de proche en proche en suivant les plaines de ce département de montagne, plus précisément le maillage routier principal. On devine en effet le rôle structurant de la route, à l’échelle locale, sur les mobilités professionnelles iséroises qui sont fortement contraintes par les massifs montagneux.

5 La métrique mixte, fondée sur la proximité de voisinage spatial de flux locaux

Le franchissement de la limite de zone est en réalité un cas particulier d’utilisation de la notion de contiguïté, pour représenter les flux s’exprimant dans leur voisinage immédiat, parce qu’elle mobilise une métrique ordinale de plus proche voisin.

Il est effet possible de construire une matrice de k-contiguïtés (ou matrice de poids spatiaux) fondée sur une métrique continue de plus proche voisin, telles celles utilisées dans les analyses de régression spatiale. Dans ce cas, la proximité s’appuie sur la notion de voisinage ainsi que sur celle de contiguïté, elle mobilis une métrique continue (la distance kilométrique) et ordinale (k plus proches voisins).

Réalisée dans le cadre d’une approche qu’on qualifie de mixte à la fois, discrète et continue, elle mobilise le barycentre géométrique des zones d’OD spécifique au cadre d’analyse des flux OD ordinaires, mais deux raisonnements sont possibles pour sa mise en œuvre, selon que l’implantation spatiale géométrique est bi-ponctuelle (comme dans le cas des flux OD) ou bien linéaire, comme pour les flux OD affectés sur réseau^[4], mais cette possibilité ne correspond pas à notre cadre d’analyse.

Dans notre cas des flux OD ordinaires, la méthode conduit à sélectionner les flux locaux de proximité observés dans un voisinage spatial ou métrique, la méthode requérant une mesure de distance continue, exprimée en kilomètres, qui peut être associée à une mesure ordinale. Elle diffère nettement des flux locaux de proximité observés dans un voisinage territorial.

Les deux graphes de voisinage territorial et spatial diffèrent également fortement dans leurs motifs ce qui ne sera pas sans conséquences sur la représentation des flux à venir. Pour illustrer leurs différences la Figure 9 présente une matrice d’exemple composée de huit lieux (A, B, C, D, E, F, G) dans une géométrie aréolaire et ponctuelle, les deux matrices de voisinage territorial et spatial associées, et, les deux graphes correspondants sont représentées pour un même ordre de contigüité k=1.

Figure 9. Illustration de la différence entre les graphes fondés sur un voisinage territorial et spatial

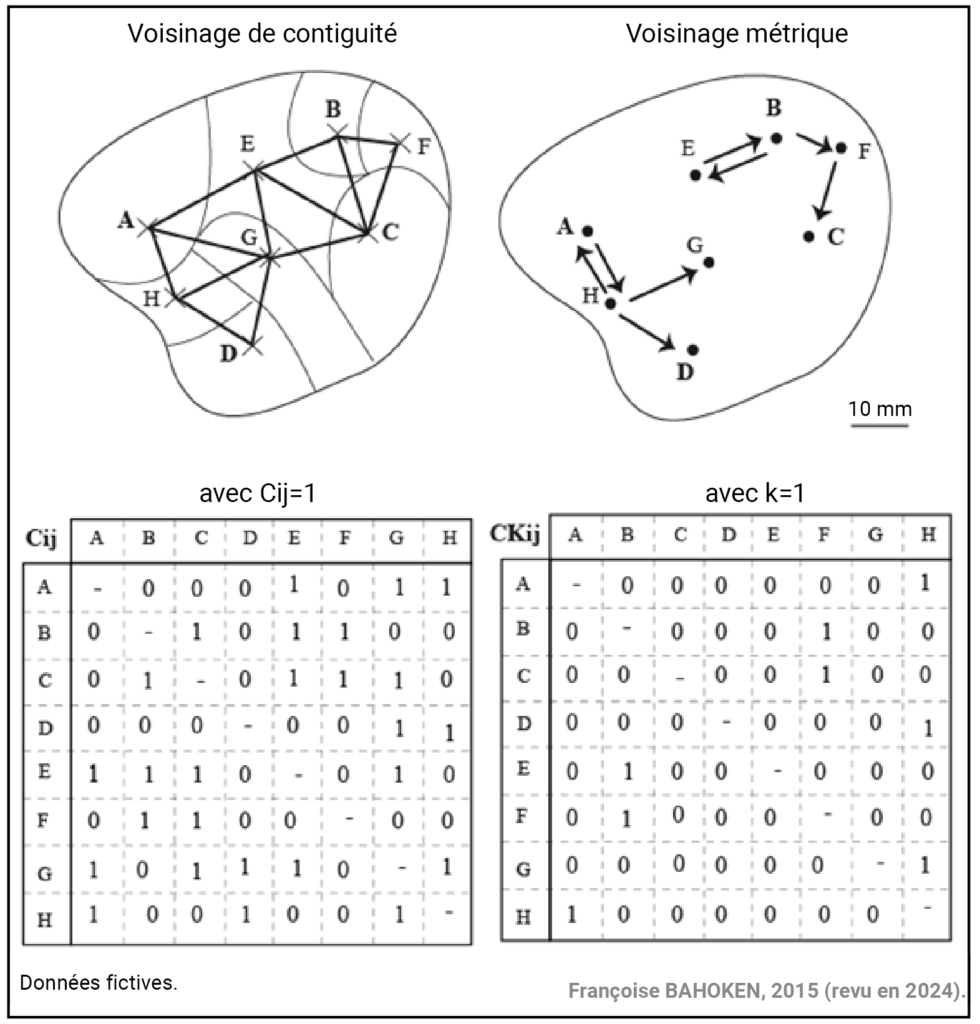
La partie gauche de la Figure 9 représente le voisinage territorial de contiguïté simple, celle de droite représente de voisinage spatial ou métrique.

La première différence visible sur les graphes, tient au nombre de liens représentés pour chacun des lieux (ou des OD) : celui de droite ne retient qu’un et qu’un seul voisin par lieu d’intérêt, à savoir le plus proche (voisin) en distance kilométrique, tandis que celui de droite en retient potentiellement plusieurs, tous ceux avec lesquels le lieu est limitrophe (et cela dépend de la morphologie du maillage).

La seconde différence tient au caractère symétrique ou non des matrices sous-jacentes, par rapport à la diagonale principale : la matrice de voisinage territorial (partie gauche) est par définition symétrique (A est adjacent à E et inversement) à l’inverse de celle de voisinage spatial (partie droite) qui est orientée – ce qui justifie l’usage des flèches sur le graphe correspondant. Cela revêt une conséquence forte : les plus proches voisins d’un lieu (i) donné ne sont pas les mêmes en fonction du type de voisinage territorial/spatial. Dans le premier cas, A possède trois plus proches voisins (E, G et H), alors qu’il n’en a que (le lieu H) dans le second cas.

La troisième différence découle également du caractère symétrique ou non de la matrice d’adjacence. Celle de voisinage spatial engendre l’élimination de certains lieux de l’analyse des flux, certains d’entre eux n’étant le plus proche voisin de personne, quand bien même ils seraient limitrophes ; c’est le cas du lieu C par exemple (F est le voisin de C, mais pas l’inverse).

Les cartographies de ces graphes de voisinage des communes de l’Isère présentent, elles aussi, des motifs de flux locaux complètement différents en fonction du type de voisinage (voir Figure 10).

Figure 10. Comparaison des graphes de voisinage d’ordre 1 de l’Isère, en fonction du paradigme continu/discret

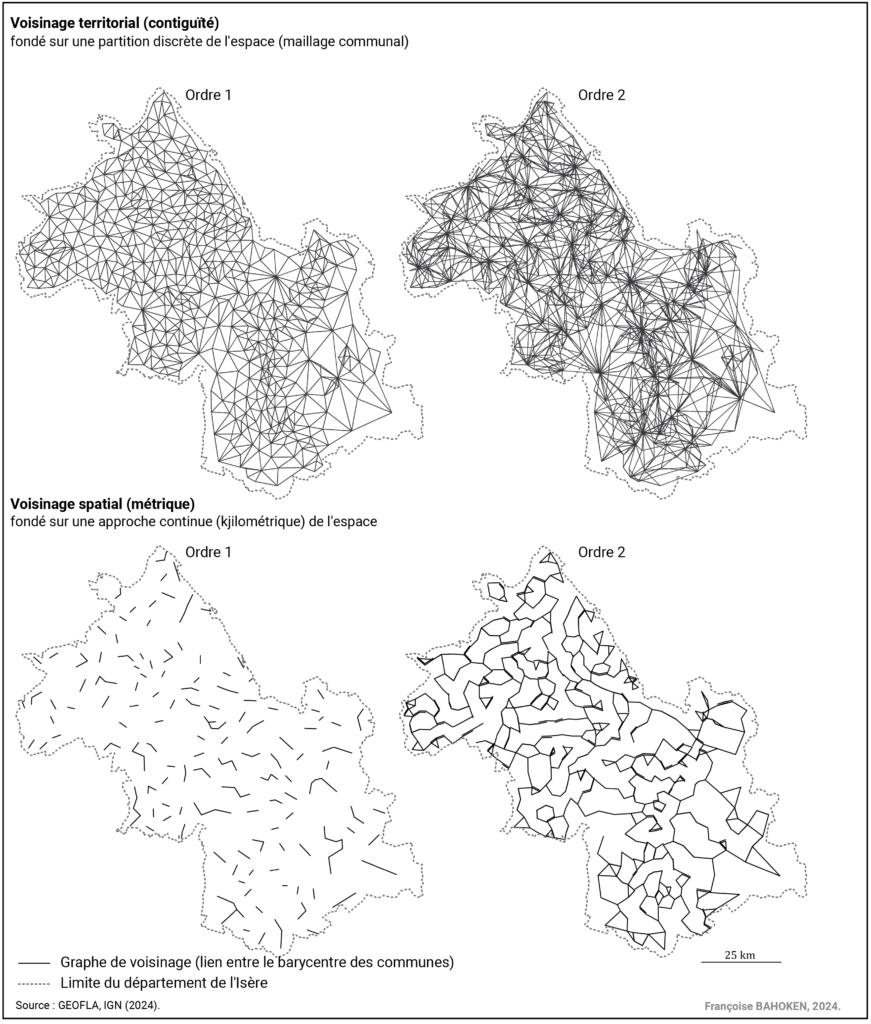
La Figure 10 ne présente qu’une parmi plusieurs possibilités de construction du voisinage spatial appréhendé par la distance euclidienne la plus courte, dans son application aux flux OD. D’autres possibilités sont envisageables en transférant les méthodes utilisées en écologie qui mobilisent différentes formes de maillage (administratifs ou théoriques comme les polygones de voronoï par exemple) et plusieurs conditions de voisinage.

Il est également possible de choisir l’orientation en degré de la direction de recherche du plus proche voisin ou encore de la distance kilométrique à un nombre k de plus proches voisins, définissant alors des k-contiguités à la manière des possibilités de déplacement d’une Reine sur un échiquier.

6 Conclusion

La manière de représenter la proximité, sur les cartographies des mobilités par des flux nécessite la prise en compte de l’espace géographique. Cependant, la manière dont l’espace de ces mobilités est appréhendé, sous une forme discrète ou continu, de même que l’acception de la proximité n’est pas sans conséquences sur le résultat cartographique.

Si l’espace géographique, via l’implantation spatiale géométrique qui sert de support à la carte, joue un rôle fondamental pour définir le flux, par la notion de franchissement de limite de zones ; cette notion sert également dans l’appréhension du voisinage de flux locaux, selon qu’ils s’expriment entre des zones qui sont adjacentes ou non, du moins proches (jusqu’à l’ordre 4), c’est-à-dire que l’espacement des OD est défini en termes de contigüité simple ou non ; ou que cet espacement est une fonction de distance continue.

La cartographie de flux proches présentée a toujours mobilisé une acception de la séparation des lieux OD qui a conduit à la construction de trois matrices d’éloignement/proximité des OD devant servir à filtrer les flux à représenter. Cela signifie que les mobilités de proximité ont été filtrées par l’acception de l’espace ou du territoire traversé par des flux.

Une possibilité supplémentaire de prise en compte de l’espace dans cette cartographie de flux de proximité aurait pu être envisagée, celle où la matrice de flux est contrainte par une partition déjà existante de l’espace d’étude, par exemple des zones ou des régions économiques, linguistiques, culturelles, historiques. Il s’agirait alors de filtrer les flux à représenter pour ne retenir que ceux qui se sont produits entre des zones qui sont proches, non pour être plus ou moins limitrophes ou situés à courte distance, que pour présenter une caractéristique d’appartenance commune.

Références bibliographiques :

Bahoken F., 2022. « Représenter la mondialisation par des flux, le rôle de la distance cartographique perçue ». M@ppemonde, Maison de la géographie, 29 p.

Bahoken F., 2017. « La cartographie d’une sélection globale de flux, entre ‘significativité’ et ‘densité’ », NETCOM : Réseaux, communication et territoires / Networks and Communications Studies, 2017, 30 (3/4), pp. 315-340.

Bahoken F., 2015a. « Éléments pour une représentation (carto)graphique des matrices de flux », M@ppemonde, n°115, 16 p.

Bahoken F., 2015-b, « L’approche cartographique de la décomposition des matrices de flux », M@ppemonde, Maison de la géographie, 2014, 3 (115), 16 p.

Bahoken F., 2014. « L’intérêt du raisonnement logique dans l’analyse cartographique des flux : L’exemple de migrations internes », Revue Internationale de Géomatique, 2014, 24 (2), pp 231-249. ⟨10.3166/rig.24.231-249⟩.

Lebart L., 1969. Analyse Statistique de la Contigüité, Publications de l’ISUP, n°XVIII, pp. 81-112.

L’Hostis A., 2014. Le détour, la pause et l’optimalité, Essai sur la distance et ses apports au transport et à l’urbanisme, Mémoire d’Habilitation à diriger des recherches, Université Paris-Est-Marne-La-Vallée.

L’Hostis A., Menerault P. & Decoupigny C., 2004. « Assessing spatial planning policy with accessibility indicators: the case of Lille’s metropolis scenario », in: Advances in spatial sciences, Transport developments and innovations in an evolving world, Springer, Berlin, pp. 293-312.

Orfeuil J-P., 2015. « Vers des transports amoureux du climat ? », in Revue Projet, 2015/1 (N° 344), pp. 27-36.

Pumain D., & Saint-Julien T., 2005. Les interactions spatiales, Armand Colin, Coll. Cursus, Géographie, 191.

Tobler W. R., 1970, « A computer movie simulating urban growth in the Detroit region », Economic geography, vol. 46, pp. 234-240

Tobler W. R., 1987, « Experiments In Migration Mapping By Computer », in: Cartography and Geographic Information Science, 14(2), pp. 155-163.

^[1] La distance empirique (Eij) est celle observée dans la réalité ; la distance euclidienne (Dij) ou distance à vol d’oiseau est une forme générale et simplifiée de la distance empirique ; la distance cartographique est la forme perçue sur la carte de la distance parcourue (Lij).

^[2] Les discrétisations utilisant la courbe clinographique ont « (…) comme particularité de tenter d’associer simultanément caractéristiques thématiques et caractéristiques spatiales. Elles sont donc importantes pour la cartographie, mais deux observations sont à faire à leur sujet : d’une part, elles prennent en compte l’espace, sous son effet quantitatif et non sous son aspect qualitatif – la quantité d’espace couverte par le phénomène et non la répartition du phénomène – et, d’autre part, elles ne peuvent être utilisées que si la surface a une signification » selon Mackay (1955) cité par (Cauvin et al. 1987 : 48).

^[3] Cauvin et al. (xxx) retinrent six familles de discrétisation (segmentation dans un objectif de cartographie thématique) issus des travaux de Evans (1977) qu’ils adaptèrent pour l’occasion à savoir : « les discrétisations intuitives, arbitraires ; les discrétisations exogènes ; les discrétisations mathématiques : les discrétisations statistiques et probabilistes : les discrétisations graphiques ; les discrétisations expérimentales »

^[4] Cette approche mobilise une distance géodésique, c’est-à-dire au nombre de liens qu’il convient de parcourir pour aller d’un point à un autre

Pour citer cet article :

BAHOKEN Françoise, « Cartographier les mobilités spatiales locales par des « flux de proximité » », 4 | 2024 – Représentations de la proximité, GéoProximitéS, URL : https://geoproximites.fr/ark:/84480/2024/12/23/rp-al2/